Dark Sausages and Effective Operators
By Shawn Westerdale, January 22, 2020
Article: “Implications of the Gaia Sausage for Dark Matter Nuclear Interactions”
Authors: Jatan Buch, JiJi Fan, John Shing Chau Leung
Reference: https://arxiv.org/abs/1910.06356 [hep-ph]
I’ve posted about dark matter before, and so it should come as no surprise to most readers here that dark matter is extremely mysterious. To make things even more mysterious, it turns out there is some compelling evidence that a large fraction of the dark matter in the Milky Way is in a giant sausage.

Figure 1. A 100% accurate depiction of a large fraction of the dark matter in the galaxy.
Normally, when people talk about dark matter, they make a bunch of assumptions. These assumptions can be broken down into two groups, which underlie most of what we say about dark matter, based on experiments and observations:
- What are the velocity and spatial distributions of dark matter?
- How does dark matter interact with itself and the Standard Model?
In the field of direct detection, we typically care about the distribution of dark matter in the Milky Way local to the sun and how dark matter interacts with nuclei (or, for some experiments, electrons).
All of this information is encapsulated when we predict the number of signals we expect to see in a detector with the equation:
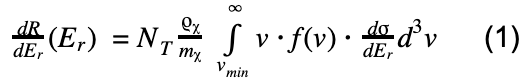 , where NT is the number of target nuclei in the detector, Er is the recoil energy of a given scattering event, ρχ/mχ gives the number density of dark matter particles near the earth (the local dark matter density divided by the dark matter’s mass), f(v) is the velocity distribution of dark matter particles in the Earth’s reference frame, and dσ/dEr is the differential scattering cross section for dark matter particles on the target nucleus. These last two terms encapsulate the astrophysical and particle physics models, respectively.
, where NT is the number of target nuclei in the detector, Er is the recoil energy of a given scattering event, ρχ/mχ gives the number density of dark matter particles near the earth (the local dark matter density divided by the dark matter’s mass), f(v) is the velocity distribution of dark matter particles in the Earth’s reference frame, and dσ/dEr is the differential scattering cross section for dark matter particles on the target nucleus. These last two terms encapsulate the astrophysical and particle physics models, respectively.
For a long time, we’ve had observations of the Milky Way that we can use to infer the local density ρχ, though there are significant uncertainties associated with it. It is also common to assume that the velocity distribution f(v) is described by an isothermal halo whose dispersion matches that at the local standard of rest. What that means, more or less, is that we live in a giant cloud of dark matter particles (called the halo), where each particle is traveling in a random direction in the galactic rest frame. We assume the speed follows a Maxwell-Boltzmann distribution where the spread is given by the “typical speed” of stars at some distance from the center of the galaxy. When we boost from the galactic rest frame to the rest frame of the Earth, the dark matter particles then pick up a net average velocity moving towards the Earth. If you’re interested in learning more about this model, typically called the Standard Halo Model (SHM), there’s a pretty clear explanation of this model in this paper by C. McCabe.
The particle physics model factors into the dσ/dEr term. This term describes the differential cross section for dark matter particles scattering off of an entire nucleus, which is built by scaling the dark matter-nucleon cross section to the entire nucleus. This scaling depends on the nuclear physics of the target nucleus and the nature of the dark matter-nucleon coupling (e.g. does the interaction scale with the spin of the nucleon or its orbital angular momentum?). Without knowing much about dark matter, it is hard to constrain the space of possible interactions too tightly. However, a number of theorists have taken an effective field theory approach to writing out a finite list of all possible interaction terms that the Standard Model might permit. This approach is described in several different papers, including this one by A. Fitzpatrick et al. When we constrain dark matter-nucleon couplings, it is typical to assume one of two types of interactions: spin-independent or spin-dependent couplings.
Realistically there’s no reason to expect that dark matter interacts via these two particular couplings out of the 15 permitted by the effective field theory framework, but they are the simplest to write down. As a result, there has been a growing interest in exploring how existing null results can constrain these other interactions as well, including studies recasting limits from XENON100. These studies allow us to constrain the broader scope of dark matter searches to all possible interaction types, which have different functional forms for dσ/dEr.
It’s worth noting that some of these interactions introduce terms into the differential scattering cross section that are proportional to the dark matter velocity squared. Given this dependence, one might expect some interaction types to be particularly sensitive to uncertainties in the astrophysical model.
The world of Gaia
While a number of astrophysical observations have accumulated over the years to indicate that the SHM may be incomplete, a recent trove of data released by the European Space Agency’s Gaia spacecraft has spurred a sort of Renaissance in these studies with a massive catalogue of stars and their velocities.
This release is just a few years old, and already there have been several interesting studies of its implication. One interesting study by L. Neicb et al. showed that in simulations of galactic mergers, where mass from one galaxy is eaten by another, the dark matter spatial and velocity distributions are strongly correlated with those of the accreted stars. This correspondence means that we can use stellar distributions to infer dark matter distributions.

Figure 2. Artistic rendition of a galactic merger, with stellar and dark matter accreting into the larger galaxy. Image modified from NASA and Hubble Heritage Team
This process is illustrated in Figure 2, where we see matter accreting from one galaxy to another during a merger event. Necib et al. showed that by measuring stellar populations from these merger events, identifiable by younger stars with velocity and spatial distributions that differ from the primary SHM, we can infer the distributions for dark matter accreted in the same merger event.
How the Sausage is made
With the release of the Gaia data, a number of potential stellar substructures have been discovered, which may correspond to stars accreted during various merger events during the galaxy’s history. One particularly prominent feature that has been identified is a population of young stars with relatively narrow velocity distributions in the θ– and φ-directions, but a very broad distribution in the r-direction. This creates a sausage-like shape in velocity-space, garnering the population the name “Gaia Sausage” (or, sometimes, “Gaia enceladus”).
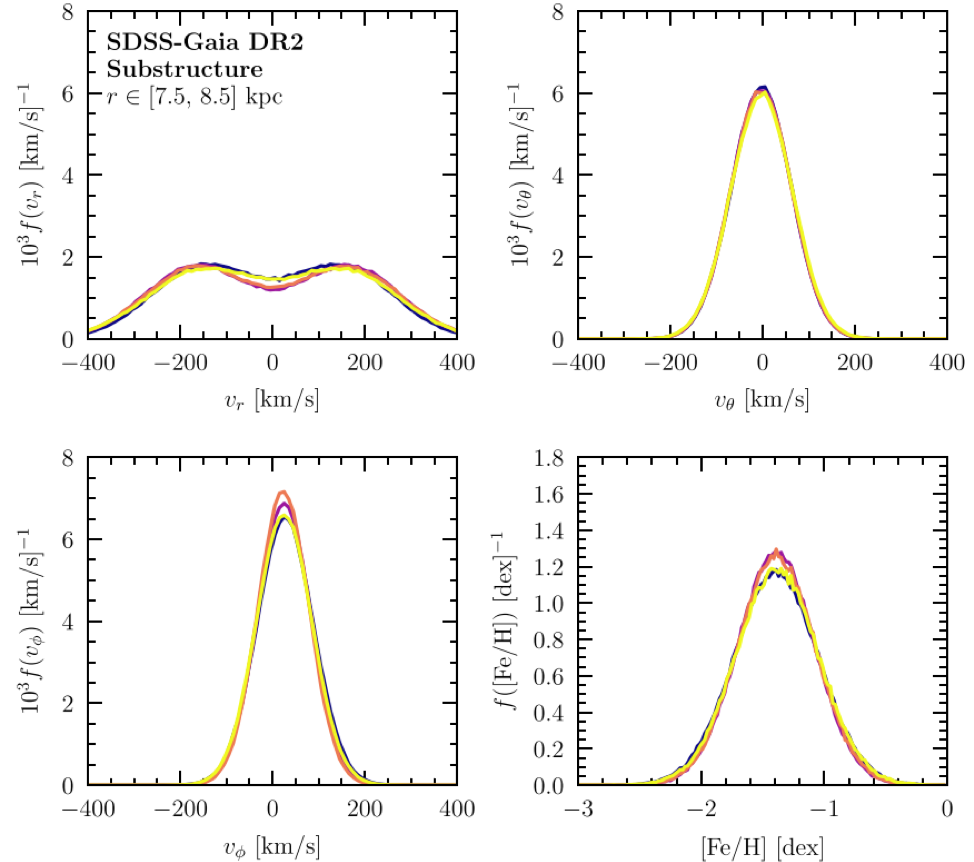
Figure 3. The inferred galactocentric velocity distribution and metallicity of the stars identified as belonging to the substructure observed in the Gaia data, referred to as the Gaia Sausage, from Necib et al.
Figure 3 shows the inferred velocity distribution of the stars in the Sausage, from Necib et al. Other groups have taken different approaches to inferring the shape of the velocity distribution, including Evans et al. The end result has generally been that the stars in this substructure (and therefore the dark matter) have a slightly slower and narrower velocity distribution in the Earth-frame. Since the spread in the velocity is in the r-direction, perpendicular to the Earth’s motion through the galaxy (mostly in the φ-direction), the large spread does not get boosted by the change in coordinates to the Earth-frame.
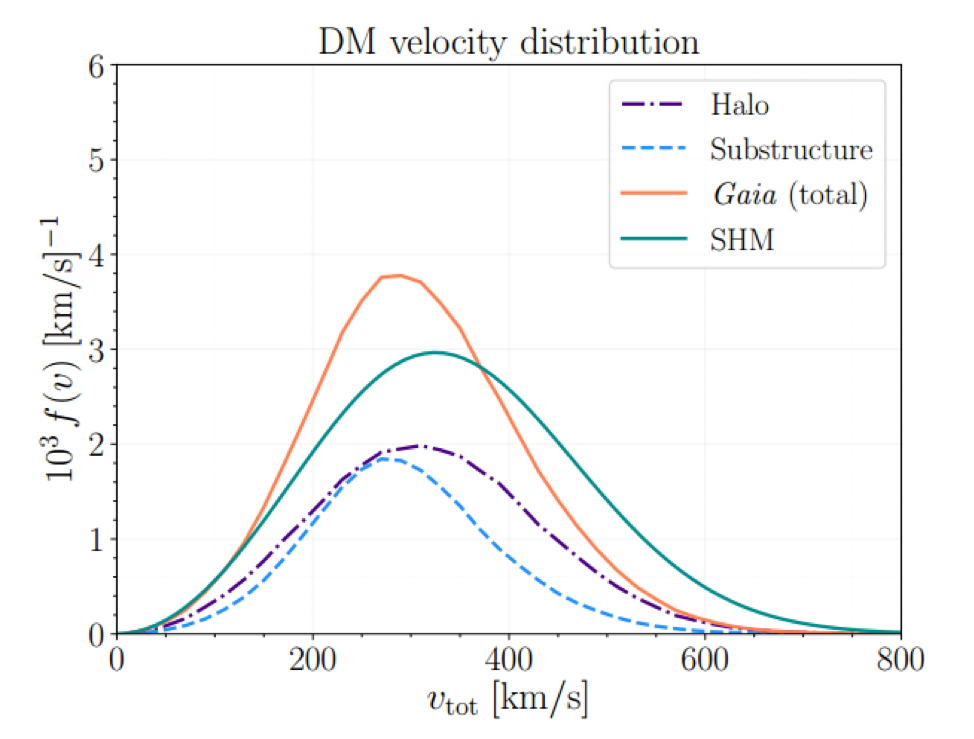
Figure 4. The inferred velocity distribution of dark matter in the galaxy, accounting for the standard halo (labeled “Halo”) and dark matter contained in the Sausage (labeled “Substructure”), compared to the pure SHM. Take from the paper.
The Earth-frame velocity distribution is shown in Figure 4. We can see that accounting for this new component results in a slower and narrower velocity distribution. The biggest difference between this distribution and the one suggested in Evans et al. is the fraction of dark matter in the Sausage. Necib et al. suggest that 44+26-22% of the dark matter in the galaxy is in the Sausage, while Evans et al. suggest a value closer to 20 ± 10%.
On sausages and operators
Finally, the paper cited at the beginning of this post explores how the possible Gaia Sausage might impact our ability to discover dark matter that couples to nucleons via different effective operators.
This paper starts with a clearly-written review of the different effective field theory operators and how they modify the recoil spectra for different dark matter masses, both for the pure SHM and for the new model combining the SHM with the Gaia Sausage.
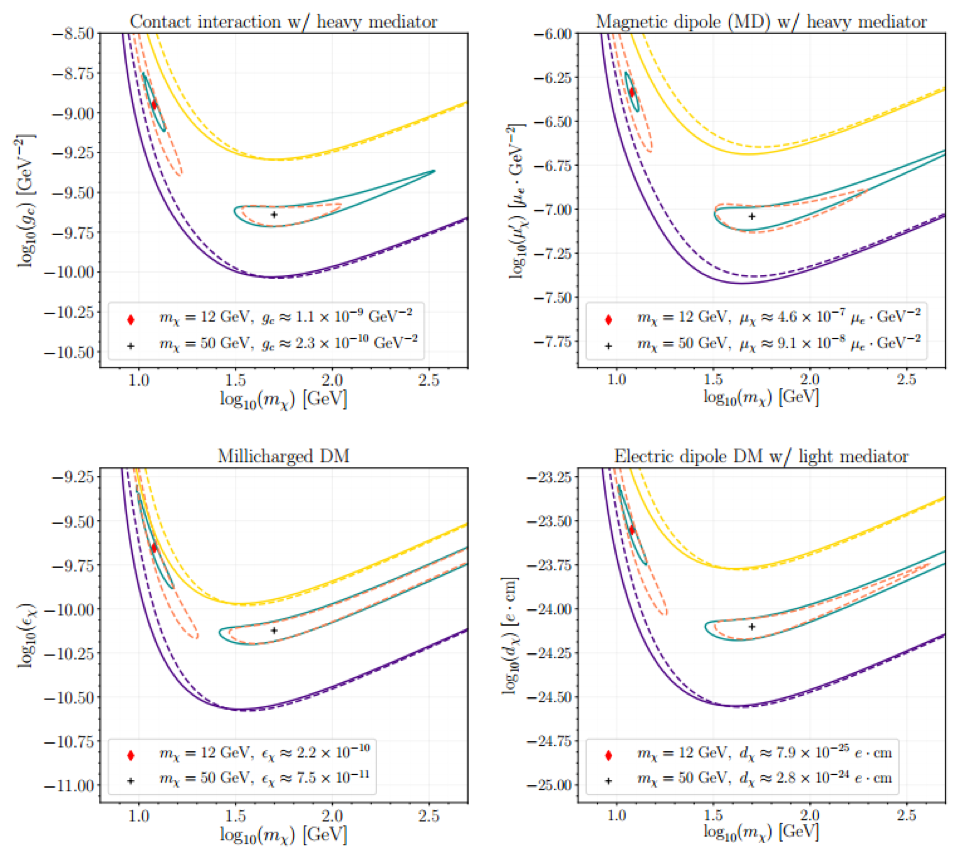
Figure 5. Results from a simulated liquid Xenon (LXe) experiment, showing sample 90% C.L. upper limits and 68% C.L. discovery contours for two example dark matter masses and coupling constants for four different interaction types. These contours are drawn for the SHM (solid lines) and for the Gaia-derived model (dashed lines), showing how a few possible interactions allow for different constraints in mass vs. coupling constant-space. Taken from the paper.
This paper has several illustrative plots that show how the Gaia Sausage impacts our ability to resolve different interaction types. Figure 5 demonstrates this by showing example exclusion curves made in a simulated liquid Xenon (LXe) detector for the SHM and the Gaia-derived halo+Sausage model, showing how exclusion curves change with the change in the velocity distribution. This figure also shows two mass vs. coupling constant contours for two hypothetical dark matter discoveries, with different masses and cross sections, and how well such a detector can constrain the dark matter’s properties. Depending on which velocity distribution one assumes, different constraints may be placed.
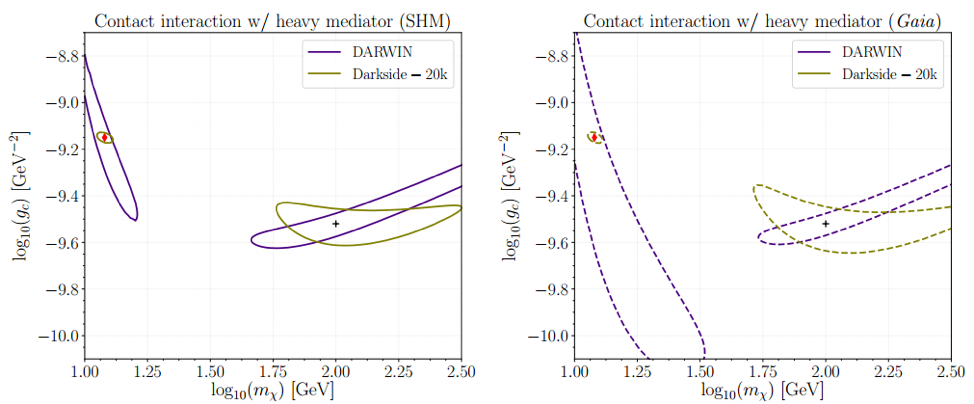
Figure 6. Simulated dark matter discoveries in a future large LXe detector (DARWIN) and a future large liquid Argon (LAr) detector (DarkSide-20k) for two example dark matter masses and coupling constants, showing how the measured constraints differ for the SHM (left) and Gaia-derived model (right), for one particular interaction type. Taken from the paper.
Figure 6 explores this further for one particular interaction type (a contact interaction with a heavy mediator) in liquid Argon (LAr) and LXe detectors for both velocity distributions. This figure shows that, for a dark matter particle with some given mass and coupling constant, LAr and LXe detectors place different constraints on the particle’s properties that compliment each other, and that these constraints vary differently under the SHM and the Gaia-derived model. The authors point out that this shows that signals observed with different target nuclei can be used to constrain astrophysical uncertainties as well as the particle physics uncertainties.
This paper is one of the first attempts to simultaneously explore the effects of both the astrophysical and particle physics models on direct detection dark matter experiments, building on the interesting observations that have been made in the latest Gaia release. Their results show that our ability to constrain dark matter’s properties, including how it interacts with nucleons, depends on potential dark substructures that may have accreted into the galaxy. They show that these dependencies are different for LAr and LXe detectors, emphasizing the complementarity of different detector technologies. If we do discover WIMP-like dark matter in the near future, we will need observations with multiple target nuclei in order to really determine its properties.


About Shawn Westerdale
I am a postdoctoral fellow at Carleton University in Ottawa, working on the DEAP-3600 direct dark matter detection experiment. I completed my PhD at Princeton, working on the DarkSide-50 experiment. And before that, I worked on the MiniCLEAN experiment for my bachelors at MIT. As a hipster physicist, I was into dark matter detectors when they were still underground.
