Goldstone Boson Becomes Dark Energy … and later also Dark Matter?!
Post by new contributor Islam Khan, October 24, 2019
Article: “Cosmology with Ultra-light Pseudo-Nambu-Goldstone Bosons”
Authors: Joshua A. Fireman, Christopher T. Hill, Albert Stebbins, and Ioav Waga
Reference: arXiv:astro-ph/9505060
What dominates the present energy density of the universe? You may have heard that it’s mostly dark energy. But, what exactly is dark energy? It’s probably Einstein’s cosmological constant, right? Do we have any clues about the source of this constant that drives the late accelerated expansion of the universe? That is where things start to get complicated. The possibilities for the source of dark energy are (literally) infinite: It could be anything ranging from a very fine-tuned vacuum energy density to the unsolved correct theory of quantum gravity, or a combination of multiple sources. On top of that, about 24% of the universe is made up of the mysterious dark matter. Out of all of the possible theories to explain these dark sectors, one popular source is that of a Goldstone boson (or Nambu-Goldstone boson) field with very light mass, associated with spontaneous and explicit symmetry breaking in quantum field theory (QFT). The implications of this light Goldstone boson on cosmology was laid out in this paper by Joshua Fireman, Christopher Hill, Albert Stebbins, and Ioav Waga in 1995. In today’s post, we will be discussing the model used in that paper and how this hypothetical field can simultaneously manage to solve both the dark matter and energy problems.
The Standard Model of Cosmology and Endless Problems
There’s no arguing the standard model of cosmology provides excellent fits with the observations. The most likely candidate would be the summed zero-point energy of quantum fields. However, calculations show there’s a discrepancy of at least 55 and up to 120 orders of magnitude between the theoretical prediction and observation. This is popularly known as the cosmological constant problem and it has been called the worst theoretical prediction in the history of physics. One appeal of supersymmetry is that it provides a mechanism for these zero-point energies to cancel. While appealing, there remains a fine-tuning problem that the cancellation should not be exact: an extremely fine-tuned non zero leftover energy density is required to explain observations. It also seems very mysterious and coincidental that, while having different sources of origin, the energy densities of dark matter and energy presently have the same order of magnitude. Unless you’re a true believer of the unsettling anthropic principle (or given up), you’re likely to be looking for answers in every possible direction.
When There’s a Field, There’s a Potential
You may have already heard at some point that there is something even more fundamental than the elementary particles of the Standard Model. All particles that we see around us are nothing but excitations of their corresponding underlying fields (that are permeating all of space-time). Likewise, the Higgs boson was only detected when the Higgs field was excited enough by colliding protons together at the Large Hadron Collider (LHC). Just as the Higgs field can be represented by a ball on a “Mexican hat” potential, any scalar field can be modeled by placing it on a potential with a specific shape. Similar to a ball rolling down a hill (Figure 1), potential energy is stored in the field when it’s high up the hill which gets converted to kinetic energy as it rolls down.
Figure 1. The scalar field rolls on its corresponding potential the same way a ball rolls down a hill. Image credit: Mr. Torgerson’s 6th grade class.
The well-known inflation theory is also modeled by a scalar field, the “inflaton”, rolling down a potential. That being said, the model described in this paper is that of a scalar field corresponding to a hypothetical particle known as a pseudo-Nambu-Goldstone Boson (pNGB), which is sitting on a potential with the form: V(φ) = M4[1 + cos(φ/f)], characterized by the two mass scales M and f. The authors claim these scales have relevance within particle physics, meaning they are not totally random numbers. The M (∼10-3 eV) has a value comparable to light neutrinos (the current upper bound is ∼1 eV), whereas the f (∼1018 GeV) is comparable to the Planck energy scale. Each of these values correspond to mass scales where symmetry breaking take place.
Breaking of Symmetries
Suppose there is a perfectly round sphere in front of you and you are asked to close your eyes. Once you open them, would you be able to tell if someone had rotated the sphere or not? It is said to have (3-dimensional) rotational symmetry. Various types of symmetries can exist and there are mechanisms that can break them, for instance, Spontaneous Symmetry Breaking (SSB). SSB appears in many branches of physics, such as the Standard Model, superconductivity, superfluidity, and Bose Einstein Condensation (BEC). To understand SSB, think of a round dinner table set at a banquet as shown in Figure 2.

Figure 2. As soon as a guest takes a napkin from either the left or right side, the symmetry is spontaneously broken.
There are napkins placed between each pair of neighbors. Everything is perfectly symmetric, until one of the guests take a napkin from either the left or right side, determining the choice for everyone else at the table, consequently breaking the rotational symmetry. SSB was first discovered in the field of superconductivity: as a material becomes a superconductor (when the temperature falls below some critical value), it slows down the penetration of electromagnetic fields through it and the photons appear to have acquired “mass”. Yoichiro Nambu was the first to realize SSB also applies in particle physics by showing it could take place in empty space in the presence of a field. A famous example of SSB is the one in the Higgs mechanism where the Higgs potential symmetry is spontaneously broken at the electroweak energy scale as the universe cools down.
As you can probably tell, breaking of any type of symmetry has consequences. The Goldstone’s theorem states that when a global continuous symmetry, another type of symmetry like the rotational one, is spontaneously broken, it gives rise to massless Goldstone bosons. The Higgs mechanism involves SSB (of an exact potential) producing massless Goldstone bosons due to the Goldstone theorem. Those bosons, however, disappear from the theory as they are absorbed (or “eaten” away) to give the W and Z bosons their masses. You may be wondering what this has to do with dark energy particles. Well, there is a second step of symmetry breaking at play here known as explicit symmetry breaking (ESB). Instead of starting with an exact symmetry, if we have an approximately symmetric one, (in other words, if there is an external force causing the potential to be slightly tilted in one direction), the Goldstone boson will acquire a tiny amount of mass. The Goldstone boson in this paper is the pNGB where the “pseudo” refers to their light mass. The boson’s mass can be determined from the SSB and ESB mass scales. If you have come across “axions” at any point, you would be happy to know they are also pNGBs and so are the pions (π mesons). They also acquire a small mass by the same mechanism and can be characterized by the two corresponding symmetry breaking scales. Each of them have different masses since their symmetries are broken via different sources.
Cool, but How Do They Solve the Problems?
We will first have to make an audacious assumption: The total zero-point energy density of the universe is zero due to some unknown symmetry. If there exists a field which is not at the minimum of its potential (assuming V(φ) = 0 at the minimum for that field), its potential energy density will have implications on cosmology. The equation of motion of a scalar field, also known as the Klein Gordon equation, is given by d2φ/dt2 + 3Hdφ/dt + dV(φ)/dφ = 0, which has the exact same form as a damped harmonic oscillator, 3Hdφ/dt being the “Hubble friction” term caused by the expansion of the universe. The pNGB field is initially displaced from its minimum where it remains frozen due to being overdamped by the “friction”. The authors claim this small potential energy density of the pNGB field could be the source of the effective cosmological constant (keeping in mind the bold assumption made earlier). As the friction decreases due to the Hubble parameter decreasing over time, the field unfreezes and starts rolling down over the potential. Since the bottom of the potential is concave, the field would be undergoing damped oscillation.
An interesting property of an oscillating scalar field is that it can behave as if it were a collection of matter particles if the shape of the potential is chosen accordingly. Consequently, the oscillating pNGB field acts the same way as matter particles. To sum up the evolution, the frozen pNGB field is the source of the cosmological constant at early times and at the present it contributes to both the cosmological constant and acts as cold dark matter (CDM). Remember the coincidence problem? If the pNGB field is responsible for both dark matter and energy, it would explain their similarity in magnitude. The pNGB field model is characterized by the two mass scales M and f only. How the field behaves for the various values of the scales is beautifully shown in Figure 3.
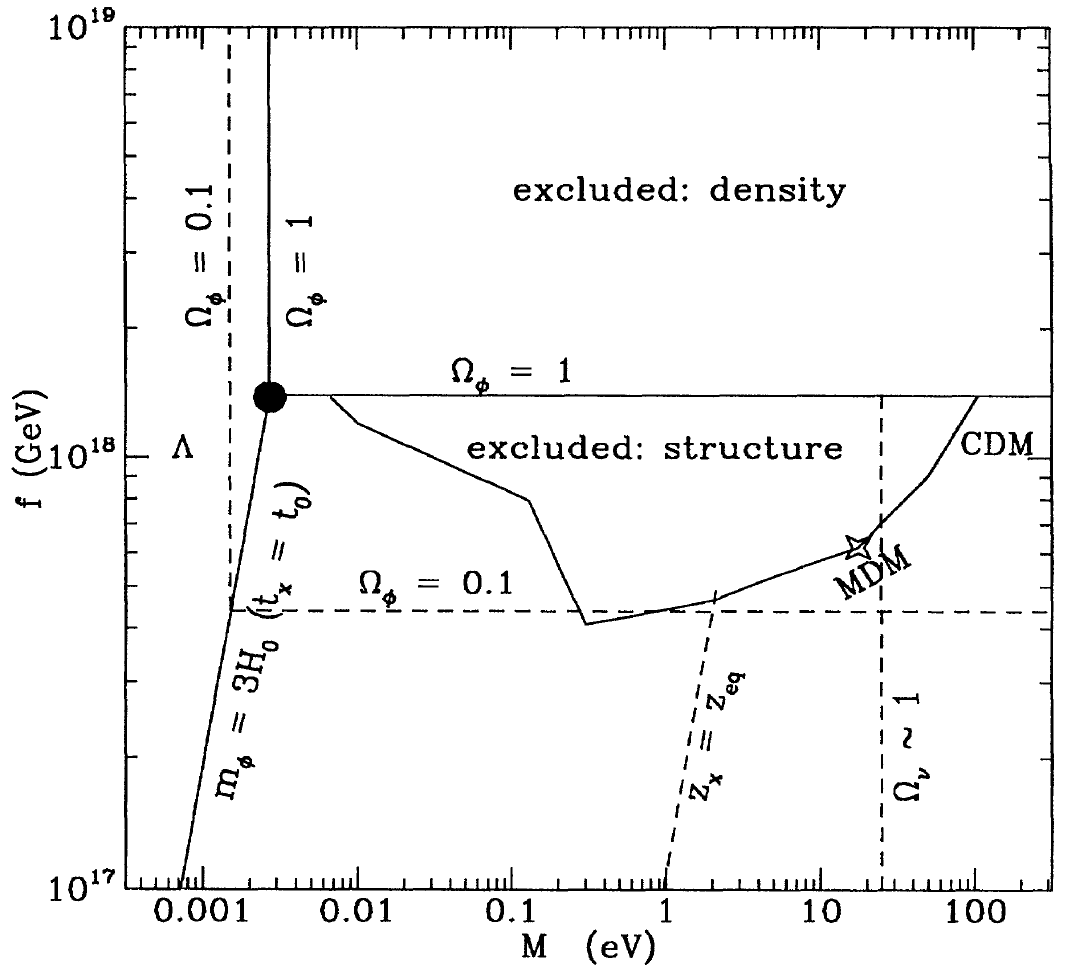
Figure 3. Figure 1 from the paper showing the pNGB model parameter space.
On the graph, tx is when the field unfreezes and becomes dynamic (undergoes damped oscillation). At the time of the paper, the observed density parameters were ΩΛ ∼ 0.6-0.8 and Ωm ∼ 0.2 for dark energy and matter respectively. ΩΛ + Ωm ∼ 1 since a flat universe had been assumed. The authors show the model being consistent with observations when the combination M ∼ 10-3 eV and f ∼ 1018 GeV were picked. The mass of the pNGB field using these values was obtained to be mφ ≲ 4 × 10-33 eV which agrees with the prediction that the field has a very small mass.
In the paper, the authors suggest that the corresponding Goldstone bosons with light mass produced by SSB and ESB are the missing dark energy particles. In the world of particle physics, we can’t think of them as particles floating in space, but as an underlying scalar field spanning all of space-time, undergoing motion on a cosine shaped potential. It was successfully shown that a model of pNGB field would be the source of the cosmological constant when it remains frozen and after it thaws to become dynamic, it would also behave as CDM. It can single handedly drive most of the energy density of the present universe. The field is characterized by its SSB and ESB scales, which are considered “reasonable” within the framework of particle physics. Quite impressive, don’t you think?


About Islam Khan
I am a PhD candidate in Physics at Washington State University and my research interest is in the field of particle cosmology. I am currently working on developing a novel quintessential inflation model, in which the energy density of the “inflaton” field that drove inflation found a way to survive until recent times to behave as dark energy. Outside of cosmology, my hobbies include traveling, playing fingerstyle guitar, and playing soccer.
