Neutrino as the Dark Force
Postdoctoral Fellow Nicholas Orlofsky and Prof. Yue Zhang propose that self-interacting dark matter can occur via the exchange of Standard Model neutrinos, instead of light dark matter force carriers. This solution enables an allowed parameter space where dark matter can influence small-scale structure in the universe, and provides a unified solution to long-standing problems in small-scale structure formation. The corresponding interactions are testable and provide targets for precision measurements at upcoming collider experiments.
6 minute read
The Gist
The search for dark matter (DM) is an active field in experimental astroparticle physics, with experiments such as DEAP-3600, DarkSide-20k, PICO, NEWS-G, SBC, and SuperCDMS attempting to observe dark matter particles. There is not, however, a unified theory for DM. With the possibility of hot, warm, and cold dark matter, each possible solution creates mismatches between what is predicted and what is observed.
Some of the problems (or puzzles, depending on your point of view) resulting from current DM theories include the core-cusp problem, the too-big-to-fail problem, the missing satellite problem, and the issue of seeding supermassive black hole formation. These are all puzzles in small-scale formation, or on the order of galaxies to galaxy clusters, relating to disparities between observations and DM models. Such discrepancies motivate investigating and testing new DM models, so as to find a unified solution that explains observations of our universe.
Postdoctoral fellow Nicholas Orlofsky and Prof. Yue Zhang at Carleton University have proposed such a solution. In their recent publication, they propose non-gravitational DM self-interaction mediated exclusively by standard model neutrinos could address the puzzles of DM and provide a testable, unified solution for small-scale structure problems.
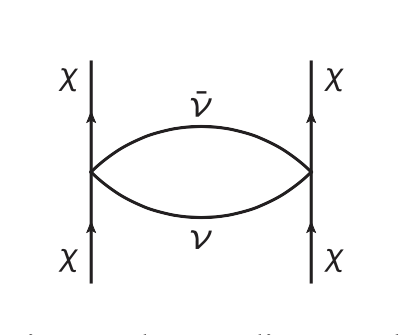
 Caption: Fig 1 from the published paper. Two-neutrino exchange diagram that can generate a long-range potential between DM particles. | DM self-interaction, which could complete with gravity and impact the formation of small-scale structures, has been well investigated but often with the introduction of light DM force carriers. Relying on the largely unknown nature of neutrinos, and specifically \(\nu_\tau\), neutrinos themselves may enable DM self-interaction. In this model, DM self-interaction would occur via the exchange of two neutrinos and forms a generic possibility within neutrino portal theory. |
The Model
Other than gravitationally, there are three possible channels through which dark matter could interact with Standard Model particles: the kinetic mixing portal (through the photon), the Higgs portal, or the neutrino portal. The neutrino portal, the focus of this work, generates an effective interacting Lagrangian:
\( \mathcal{L}_{\rm int} = y_\alpha \bar{\nu}_\alpha \chi \phi + \left( \scriptsize{\textrm{Hermitian conjugate}} \right)\),
where \( y_\alpha\) is the Yukawa coupling between the neutrino \(\nu_\alpha\), the dark fermion sinlget \(\chi\), and the scalar field singlet \(\phi\). It is assumed that the mass of \(\phi\), \(m_\phi\), is larger than the mass of the DM candidate \(\chi\), \(m_\chi\). \(\alpha = e, \mu, \tau\), representing neutrino flavours. At long-range, the potential from this interaction is
\( V(r) = \frac{|y_\alpha|^4}{128 \pi^3 (m_\phi^2-m_\chi^2)^2r^5}\).
Only asymmetric DM is relevant for this interaction, as the symmetric population of DM is efficiently depleted for the coupling values \(y_\alpha\) of interest. This implies that the potential is repulsive.
Solving for the scattering cross section with quantum mechanics gives
\( \sigma_{\chi\chi\rightarrow\chi\chi} \approx 0.027 \Big[\frac{m_\chi|y_\alpha|^4}{(m_\phi^2-m_\chi^2)^2}\Big]\),
and provides a basis for the parameter space allowed for this interaction, as seen in the figure below.
The Small-scale puzzle solution
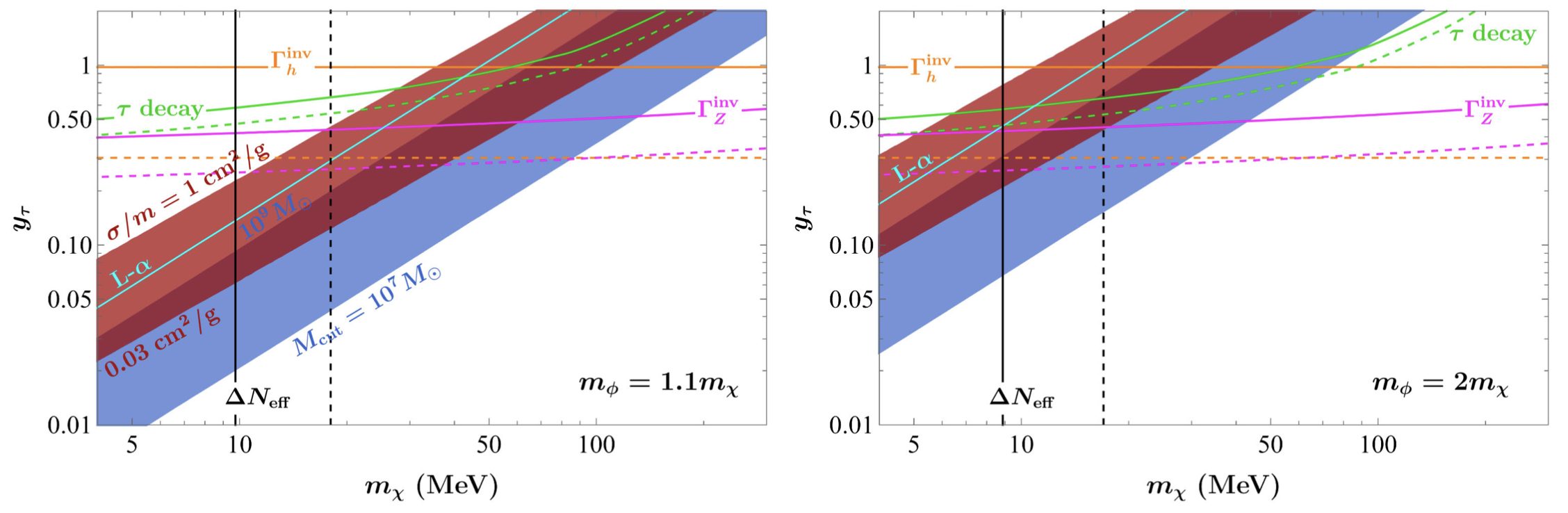
Caption: Fig 2 from the published paper. Shown is the region of parameter space where the long-range force due to neutrino exchange can generate a sufficiently large DM self-interaction cross section for addressing puzzles in small-scale structure formation. The dark red shaded band corresponds to 0.03 cm2/gram ≤ σ𝜒𝜒→ 𝜒𝜒=m𝜒 ≤ 1 cm2/gram. The dark blue band corresponds to χ serving as a warm DM. The two regions intersect in the darkest shaded region. The cyan curve sets an upper bound on neutrino-χ interactions from Lyman-α. The lower bound on the DM mass set by ΔNeff is shown by the vertical black line. Existing upper bounds on the Yukawa coupling |y𝜏| are set from the invisible decays of the Z boson (magenta curve) and Higgs boson (orange curve) and the leptonic decay of the 𝜏 (green curve). Current bounds are solid, and projected bounds are dashed. All bounds are at the 95% confidence level.
From the scattering cross section given above, the parameter space for self-interacting DM can be derived. Focusing on the the \(\nu_\tau\) neutrino as the exchange particle and using the upper bound provided by observations of the Bullet Cluster, the red shaded region in the figure above corresponds to \( 0.03 \leq \sigma_{\chi \chi \rightarrow \chi \chi}/m_{\chi} \leq 1 \rm cm^2/gram\). This region is effectively the parameter space for the solution to small-scale structure problems, like the core-cusp and too-big-to-fail problems previously mentioned.
Notably, large \(y_\alpha\) can keep DM and neutrinos in kinetic equilibrium for an extended period of time. This leads to a suppressed DM density power spectrum at small length scales via collision damping, giving a cutoff mass scale for the smallest gravitationally bound DM halo and enabling a warm dark matter scenario. The DM candidate \(\chi\) as a warm DM is represented by a blue band on the above figure, where by giving a cutoff mass scale \( 10^7 M_\odot – 10^9 M_\odot\) it would solve the missing satellites problem in addition to providing testable predictions. (\(M_\odot\) represents the Sun’s mass.)
The parameter space for a solution to small-scale structure puzzles and a warm DM scenario overlap, as shown in the above figure as a dark red band. This implies it is possible for the DM candidate \(\chi\) to meet the demands of solving all mentioned small-scale structure problems.
The Testability
The consequences of this model lead to observable measurements by upcoming experiments.
In direct relation to a warm dark matter scenario and the suppression of small-scale structure, this suppression cannot extend to large-scale structure and must have an upper bound of validity. This model can be constrained by measurements of the CMB, large scale structure, and Lyman-𝛼, of which the Lyman-𝛼 contribution is the most significant. Lyman-𝛼 sets the upper bound on the elastic scattering cross section to \( \sigma_{\rm el}/m_\chi < 10^{-36} cm^2/MeV\) for neutrino energies of about 100 eV. This upper bound is represented on the above figure by a cyan blue line within the red band, labelled L𝛼. Higher energy neutrinos set upper bounds well outside the considered parameter space.
Another outcome of self-interacting DM via neutrinos is that the excess radiation degrees of freedom, \( \Delta N_{\rm eff}\) constrains the mass of the DM to be greater than 9.7 MeV for \(m_\phi=1.1 m_\chi\) (left panel in image above) and 8.9MeV if \(m_\phi=2 m_\chi\) (right panel in image above). Specifically, the upcoming CMB S4 experiment will be able to see up to 18 MeV for \(m_\phi=1.1 m_\chi\) and 17 MeV for \(m_\phi=2 m_\chi\), and so could probe these lower mass bounds.
Lastly, the effective operator from the interacting effective Langranigan (i.e. the neutrino portal) has a measurable effect on the invisible decay width of both the Higgs boson and the Z boson. The invisible decay width is the partial width to decay channels whose products cannot be seen by detectors. The neutrino portal in this model would add new invisible decay channels to \(\nu_\alpha\), \(\chi\), and \(\phi\) in addition to the SM decay to two neutrinos. The measured invisible widths for these bosons is larger than what can be explained by known physics. Attributing this surplus to the neutrino portal for self-interacting DM provides upper bounds on the Yukawa coupling \(y_\alpha\).
In short, the DM model proposed would provide a long range, repulsive DM self-interaction potential mediated exclusively by SM neutrinos that solves small-scale structure problems and enables a warm DM scenario. This potential arises generically from the neutrino portal model, which induces interactions between SM and DM particles. These interactions allow for robust constraints on the mass scale for the dark states. The neutrino portal interaction is a well-motivated target for upcoming experiments, and if observed would confirm a solution to long-standing DM puzzles.
